¿Crees que tú modelo es suficientemente bueno?

Hace mucho tiempo, en una de mis vidas pasadas como consultor, escuché que un responsable DS de una conocida telco, le suelta un junior algo así como que una mejora de unas décimas en la curva ROC, significaba una mejora de miles o cientos de miles de euros en su caso de uso …

Bueno, sobre la curva ROC habría mucho de que hablar, sobre todo entender bien lo que significa (que aún muchos confunde con el r-cuadrado y no tiene ná que ver), pero eso lo dejo para otra sesión. Lo cierto, es que si a mí me sueltan algo como lo anterior, es muy probable que deje de considerar a esa persona como alguien que entiende de modelos y más le valga, darle un repaso a la estadística y sobre todo al sentido común, que parece ser el menos común de los sentidos.

Para empezar a hablar, vaya por delante que en estadística pocas o más bien nunca se tienen valores absolutos, prácticamente todo son variables aleatorias que siguen una distribución más o menos compleja, en algunos casos, bajo el marco de la estadística clásica y con hipótesis más o menos fuertes, se consigue conocer para un modelo, como el lineal, la distribución de sus parámetros y por tanto se tienen intervalos de confianza y todo aquello de lo que hoy no me apetece tratar.

Tanto esos modelos, como los actuales, en todos, hay variables aleatorias y la aleatoriedad es algo, que aunque se pueda controlar más o menos, ahí está y por tanto, está en los parámetros de los modelos y por supuesto en las estimaciones o medidas de su potencia predictiva, siendo la ROC un ejemplo de éstas en el caso de modelos de variable binarias

Si os vais a mi github, cuyo enlace os dejo aquí:

https://github.com/FJROAR/Ejemplo-Blog-ROC-Distribution

He dejado unos códigos muy sencillos para analizar un dataset como es el de biopsia que está dentro de la libreria(MASS) y que está bastante trillado pero, debido a que son pocos datos y variables, creo que puede valer para la explicación de este post.

Bien en ese código hay un par de funciones que he diseñado de modo no óptimo, pero que para este caso corren adecuadamente y nos va a permitir una discusión sobre la volatilidad de la curva ROC. Dichas funciones se denominan:

genera_roc_glm(seed, df) y genera_roc_knn(seed, df)

Y lo que hacen es que toman un dataframe df ya limpio (ojo, no aseguro que funcione para cualquier df limpio, la intención aquí es explicar un concepto, no hacer algo que raye la pureza informática, … ya que no soy informático), y lo dividen en el típico train-test al 70% bajo una semilla de aleatorización que se elije en seed, dando por tanto lugar en la primera función a la curva roc que se tendría bajo una regresión logística habitual y en el caso del knn sale el valor de la roc con los parámetros por defecto que tendría el algoritmo aplicado. Además para simplificar aún más la situación se toma como variable explicativa de la target a la V1 en este primer caso para ambas funciones.

Llegados a este punto, ¿qué pasa si seed = 1? En este caso se obtiene lo siguiente:

Claro, si soy forofo del 1 en las seed y siempre lo uso, podría afirmar que a nivel de predictividad el primero modelo es mejor que el segundo, y si no miro nada más, pues ala, a tratar de defenderlo. Pero claro, ahora viene el/la forofo/a del número 10 y hace le sucede lo siguiente:

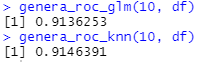
Entonces se observa que para dicho forofo/a, lo lógico sería un knn ya que su predictividad es mejor.

Bueno en este caso resulta que lo que ocurre es que la ROC es una variable aleatoria y por tanto sus valores más frecuentes estarán bajo unos intervalos cuya distribución será difícil de conocer, ya que aparte de la semilla de aleatorización, también va a depender de la separación 70-30 o 60-40 o … que se haya realizado, por tanto hacer una apuesta a un modelo en concreto porque se gane unas décima de ROC es prácticamente como tirar una moneda al aire y básicamente el histograma de cuando se generan 100 semillas y se hace la misma operación es lo que se muestra, para el caso del modelo glm y knn en el dibujo inicial. En dichos histogramas de tan sólo 100 valores (podría calcularse para más), se observa que la media y la desviación típica resultan ser las siguientes:

media glm: 0.910738 media knn: 0.906869

desviación glm: 0.016557 desviación knn: 0.018118

Nótese que gráficamente y numéricamente todo iría hacia el glm, pero claro es una muestra de sólo 100 observaciones, pero las variaciones y los saltos de valores que se da en esta sencilla distribución van desde aproximadamente 0.85 hasta algo más de 0.94 tal y como se observa a continuación:

En casos de muchas observaciones, cuando he realizado este tipo de estudios, no he visto efectos tan grandes, pero sí bastante amplios, aunque con más concentración en torno a los valores medios, con lo que hay que tener cierto cuidado cuando nos fiamos de un índice. Es cierto, que la técnica de cross-validation también puede dar una idea de cómo va a ser la variabilidad de la ROC, pero sorprende que en los proyectos de modelización, este factor no se tengan en cuenta y los que yo denomino como “preparadores de datos” que son gente que se hacen llamar DS y que lo que saben es preparar datos para meterlos en una coctelera y sacar un alto ROC o bien no se dan cuenta, o directamente no entienden los saltos que pueden dar los estadísticos que están estimando.

Y bueno, visto esto, vamos a dar una vuelta de tuerca más, supongamos que ahora en vez de 1 variable, usamos V1 y V2, a ver qué es lo que pasa si repetimos el proceso, para eso he creado las funciones:

genera_roc_glm2(seed, df) y genera_roc_knn2(seed, df)

Para no extender la exposición os hago expoiler y os dejo unas recomendaciones y consejos:

• El algoritmo puede ayudar, pero cuando se usa una variable potente, se puede pasar a otra liga, un algoritmo mejora y todos mejoran al unísono en este caso
  

• Las conclusiones se mantienen, algo más acentuadas, pero las distribuciones se superponen, hay algunos outliers, pero “no nos sacan de pobres”
  

• Este dataset está muy preparado, por eso sale tan potente, pero una vez llegado al 0.98 de ROC, poco más se va a poder mejorar
  

• Las fluctuaciones deben tenerse en cuenta, incluso en los proyecto de ML con miles de millones de datos debe controlarse los márgenes de variabilidad de la ROC, sobre todo cuando vayan a intervenir mucho dinero. Mejor dar intervalos máximo-mínimos estimados que valores cerrados que impidan la creatividad
  

• Ante modelos de predictividades parecidas, ir al más simple, si los modelos aún tienen cierta diferencia de predictividad, pero son elevadas, tomar el más simple, aunque a los “complicadores” les parecerá una “caca” porque son sencillos, os daréis cuenta que son robustos y que los podéis explicar