KNN, algoritmo lento pero interesante

Hay un par de motivos importantes a la hora de escribir este post. Uno de ellos es tratar de hacer realmente entendible qué hay detrás de un modelo tipo knn o k-vecinos más próximos (en español) y otro no menos interesante es entender porque estos modelos, cuando se aplican a grandes cantidades de datos pueden resultar lentos e ineficientes.

El modelo knn no creáis que se ha inventado con la movida del ML y demás, sino que viene de principios de los 50 y fueron desarrollados por Evelyn Fix y Joseph Hodges.

Hay muchas variantes de este modelo y aquí se va a considerar sólo 1, quizás la más avanzada que es la que creo que es más esclarecedora una vez que se entiende, así pues, se considera que se tiene una variable explicada de tipo continuo como pueda ser la variable target del conocido dataset Boston que es una estimación del precio del metro cuadrado de la vivienda en función de otras 13 variables explicativas.

Para hacer más sencillo la comprensión de este algoritmo, de las anteriores 13 variables, se van a considerar sólo 2, las denominadas RM (número medio de habitaciones) y AGE (proporción de unidades ocupadas por sus propietarios construidas antes de 1940) que se ha visto que aparecen como significativas en cualquier regresión lineal.

Dado que es un conjunto muy limpio, no hay que hacer ningún tratamiento a priori especial con estas variables. Se hace una separación training-test del tipo 80%-20% que si se representa (tranquilos, he fijado una semilla de aleatorización para que podáis reproducirlo …) se obtiene la siguiente representación siempre y cuando se haya estandarizado las variables (en el training y aplicada dicha estandarización en el test):

Observación: Tanto el anterior dibujo, como análisis que aquí se muestran están realizados bajo entorno Spyder y os lo podéis descargar de mi git en: https://github.com/FJROAR/Ejemplo-Blog-KNN

Pues vamos a entrar en materia ¿Cómo funciona esto del knn en una variable continua? Para empezar a hablar, el entrenamiento de un knn no guarda una mayor dificultad ya que prácticamente lo que se hace es “memorizar instancias” qué, ¿Qué es eso de memorizar instancias? Pues que no cunda el pánico, simplemente lo que se hace en la fase de entrenamiento es guardar (en memoria o algún sitio, …) los puntos azules (en este caso el 80% de los datos) con todos sus valores (explicativa y target) y ya no se hace nada más, como veis el tema es rápido, sin embargo, ahora llega “el momento de la verdad” ¿Cómo predice un knn cuando llega un nuevo dato? “¡Eh, amigo!, aquí la cosa, aunque creo que se va a entender, es algo más enrevesado”.

En primer lugar, debe tenerse el dato de cuántos serán los vecinos para la interpolación, en este caso supongamos que k = 1, por tanto, el primer paso a dar es calcular la distancia de ese punto a todos los puntos del training para obtener el punto más cercano posible. Una vez obtenido este punto, el valor que se interpola es el que está almacenado en el training. En el supuesto de que k = 2, se hace la misma operación hasta que se consideran a los 2 puntos más cercanos posibles y en este caso se asocia una media de valores y así sucesivamente.

Como puede observarse, aunque estas operaciones son fáciles de entender, para un procesador resulta complicado el tema de las operaciones del cálculo de distancia, ya que para cada dato debe hacer tantos cálculos como datos existe en el training y por tanto imaginaros que estamos ante un dataset de tamaño medio de unos 100.000 registros donde se aplica un 70%-30%, el número de operaciones para predecir el test sería del orden de 2100 mill y eso que para muchos esto no es más que un aperitivo en el mundo del Big Data. Además está el problema de que cada vez que entre un dato nuevo, si se pone el knn en producción habría que esperar a que haga sus 70.000 operaciones y “resto de cositas” para tener un valor, lo que puede resultar en unos segundos que en el caso de ser un proceso de entrada continuo de datos, podría hacer colapsar el sistema. Por tanto aquí está la debilidad de este tipo de modelos que hay que tenerla muy en cuenta en función del problema que se vaya a tratar.

Siguiendo con el ejemplo de los datos de Boston, aquí no se tiene este problema ya que hay tan sólo unas 506 observaciones, cuyas variables estandarizadas han sido ya representadas anteriormente separando por training y por test. Para entender lo que he dicho anteriormente vamos a ver qué es lo que hace el algoritmo exactamente. Supongamos que k = 1 y consideramos el punto del test normalizado más a la derecha:

¿Qué valor se le va a asociar? Pues bien, habiendo elegido una distancia como es la euclídea, se tiene que buscar el punto azul más cercano. Si agudizamos bien la vista, se observa que sobre el punto rojo que está al lado parece que existe un punto azul por debajo, esto se puede observar en la siguiente representación ordenada de los dataset test y training ordenados de menor a mayor por la variable RM:

El punto de interés es justamente el que tiene por índice el número 25 en el X_test_norm (buena idea esta de los índices en Python, por cierto) Y el punto más cercano a este pero en X_train_norm es el que tiene por índice el número 218, de hecho si observamos en X_test_norm, se observa que el punto que tiene por índice el número 96, tiene las mismas coordenadas que el anterior, es decir, los puntos están superpuestos y como el rojo cae encima del azul, de ahí el hecho que no se vea este último.

Pues bien, ¿Cuál es el valor que se le asociaría al punto anterior bajo un 1-nn? En este caso, dado que ya se ha averiguado el punto más cercano, se va al dataset training y es cuando se mira el valor en el target en el dataset y_train que resulta ser (buscando por el índice 218) el valor 11.9, para verlo en el código se genera una variable kpred1 donde en su valor índice 25, se obtiene dicho valor de hecho, como habrá deducido el lector, también en el índice con valor 96, el valor va a ser exactamente el mismo por razones obvias. Y ahora se da un pasito más ¿Cuál es el valor que se asociaría al punto anterior bajo un 2-nn? En este caso hay que buscar el 2º punto más cercano que resulta ser el punto azul más a la izquierda cuyo índice en X_train_norm es 165, cuyo valor de target, si se mira en y_train (en el índice 165) es igual a 27.5, por lo que la predicción a asociar en este caso en el índice 25 de y_test debe ser la media 11.9 y 27.5 que resulta ser igual a 19.7 tal y como se observa:

Llegados a este punto sabemos cómo actúa un knn y cómo asocia sus valores en el caso de una variable target de tipo continuo, pero se ha comentado que hay una limitación y es cuando el dataset es muy grande, pero ¿Y cuando tal limitación no existe? ¿Funciona bien para casos como el aquí tratado?

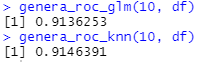
Bueno, en el código hacía una comparación usando esas mismas variables para una regresión lineal y probando con varias opciones para k, en dicho test obtuve los siguientes resultados cuando se había aplicado una estandarización de variables:

Mientras que, sin estandarizar variables, los resultados habían sido los siguientes:

Por lo que en definitiva cabe concluir las siguientes líneas generales:

-Los knn pueden dar lugar a problemas cuando se trata de modelizar datos masivos debido a que el cálculo de distancias es un proceso intensivo en cálculo, además adolecen del problema del curse of dimensionality (que no se ha tratado), con lo que son efectivos si hay pocas variables explicativas que rellenen suficientemente el espacio

-Como regla general, un preprocesado de variables es recomendable en estos modelos para que funcionen correctamente, observándose efectos muy negativos cuando las escalas de las variables son dispares

-Con pocos datos, estos modelo pueden mejorar a las regresiones lineales, pero debe hacerse comprobación con varios órdenes k, no hay regla general de elección de dicho parámetro y se recomienda en aplicaciones reales, si es que no hay mucho datos, hacer uso de cross-validaciones (que no se ha tratado aquí)

Redes Bayesianas. Aplicaciones a crédito hipotecario

Uno de los modelos que se engloba dentro de esta vorágine del Machine Learning son las denominadas Redes Bayesianas.

En mi opinión, son unos modelos aún muy desconocidos por la empresa y la verdad es que posiblemente sea porque se desconoce el potencial real que pueden llegar a tener.

Un ejemplo de red bayesiana realizada con python a través de la librería pybbn, sería el siguiente ejemplo (donde interviene notablemente la librería networkx para el diseño del grafo):

La red invención mía, y por tanto mejorable, quiere poner foco en cómo se interrelacionan algunas variables con el pago o no de un crédito hipotecario. En este caso se hacen los siguientes supuestos como:

• La edad (elevada a partir de 50 años), influye en el nivel de ahorro y en la posibilidad de tener o encontrar trabajo

• El hecho de tener trabajo influye en que se tenga un nivel de ahorro y de que se tenga o no dificultades económicas

• La marcha positiva o no de la economía influye en que sea fácil tener o encontrar trabajo y también en la marcha del sector de inmobiliario

• Finalmente el pago o no del crédito dependerá de si se tiene o no dificultades económicas y si la garantía (el bien bajo hipoteca) está bajo un mercado líquido porque el sector inmobiliario marche bien o no

La posibilidad de plantear supuestos, como se puede imaginar el lector, es prácticamente infinita y es básicamente el punto de partida de toda red bayesiana, es decir, aquí un grupo de expertos de negocio se reúne y dibuja, incluso en un papel si es necesario un grafo como el anterior.

Una vez hecho lo anterior llega el momento de darle vida, para ello hay que plantear una serie de suposiciones que pueden venir de los datos o no y justamente esto es lo grande de este tipo de modelos, la posibilidad de introducir de modo sencillo suposiciones de ocurrencia de los hechos. Así pues, en los nodos superiores se parte de probabilidades, donde el nivel de clientes de edad elevada puede ser la proporción de clientes de la entidad y en el caso de la situación de la economía, puede ser la visión que tenga de ésta el servicio de estudios, por tanto, supóngase que se tienen las siguientes tablas:

En este caso se estaría diciendo que de la población de solicitantes, la proporción de clientes con edad elevada es del 60% y que la probabilidad de que la economía tenga un año positivo es también del 60%.

Si se investiga el código, se observa fácilmente cómo este se puede manipular y poner cualquier dato en lugar correspondiente:

Ahora cabe hacer supuestos con algo más de elaboración. El nodo trabajo depende tal y como se observa en grafo anterior, de edad y economía, en este caso hay que hacer 4 supuestos (o derivarlos de los datos), como pueden ser los de la siguiente tabla:

En este caso se indica cuál es la probabilidad de que encontrar o tener trabajo sea positiva dado que, en el primer caso se tenga una edad elevada y la economía tenga una marcha positiva, siendo dicha estimación del 30%. Dicha estimación bajaría al 10% si bajo el mismo supuesto de edad, se tiene que la economía marcha de modo negativo. La anterior tabla se introduciría en python del siguiente modo sencillo:

Pues bien haciendo todo una serie de supuestos podemos introducir una estructura completa como la siguiente:

Cuya codificación en python al completo la tenéis en:

https://github.com/FJROAR/Ejemplo-Blog-Bayesian-Net

Como se puede observar, a diferencia de los árboles de decisión, aquí no se está optimizando una función para maximizar la separación de datos más o menos, aquí se implementan unos supuestos y por debajo, claro está, se aplica el Teorema de Bayes y se hace un supuesto de interrelación markoviano, de modo, que por interrelaciones, que podemos denominar, matemáticamente sencillas, podemos hacernos distintos tipos de pregunta como la que se hacen en los siguientes business cases:

BC 0: La primera pregunta sería ¿Cómo es la situación de morosidad para un desconocido que “entre por la puerta” sin mayor información sobre esta persona?

BC 1: Supóngase que las previsiones de evolución positiva de la economía son robustas y cabe esperar una evolución positiva de ésta¿Cómo afectaría lo anterior a ese supuesto cliente? evidence('ev1', 'economia', 'P', 1)

BC 2: Además de lo anterior se sabe que es una persona joven con trabajo ¿Cómo afectaría a su posible pago-impago? evidence('ev2’, 'edad', 'N', 1) evidence('ev3', 'trabajo', 'S', 1)

BC 3: Si además se tiene evidencia que el mercado de la vivienda va a evolucionar positivamente (con lo que por Markov, el tema de la economía daría igual), se tendría que la probabilidad de pago aumentaría hasta: evidence('ev4', 'vivienda', 'P', 1)

Nótese que en este último caso no se tiene seguridad de que el cliente tenga o no un colchón de ahorro, con lo que aún la duda de impago es elevada en torno a un 10%, con lo que se necesitaría tener más información al respecto o marcar un tipo de interés elevado de modo directo (o indirecto con algún tipo de comisiones)

BC 4: Sin embargo lo interesante en las redes bayesianas no es lo anterior, lo interesante es poder conocer por ejemplo elementos causales, así por ejemplo cabe preguntarse que si por ejemplo un cliente a impagado (o un grupo de éstos) ¿Cómo alteraría las previsiones a priori sobre el estado del sector de la vivienda? Se sabe también que dicho cliente tenía ahorros en el momento bajo análisis y que su edad era elevada, pero no se sabe si tiene o no ahorros en ese momento y además no se tiene evidencia sobre la situación actual de la economía evidence('ev1', 'paga', 'N', 1) evidence('ev2', 'edad', 'S', 1) evidence('ev3', 'ahorro', 'S', 1)

Momento inicial, sector vivienda:

Momento final:

En este caso se observa que debería re-actualizarse las impresiones sobre el estado de situación de la situación del mercado de la vivienda, es muy probable que el impago haya sido causado justamente por la crisis donde posiblemente se encuentre la economía (un análisis somero de la situación implicaría que lo anterior se confirmaría o habría razones para incluir nuevos elementos a explicar el impago)

En fin, sin ánimo de meterme en interpretar este ejemplo de juguete, simplemente animar al planteamiento de los problemas de negocio desde esta perspectiva, rica porque se puede introducir supuestos tanto subjetivos, como fundamentados en datos y observaciones, pudiendo crear funciones que actualicen de modo automático o manual los valores de las probabilidades totales y condicionadas de las tablas de la red. Lo complicado claro de estos modelos es que si una variable depende de muchas, el problema de decisión crece exponencialmente, por tanto son buenos cuando hay que crear un mapa conceptual sencillo y se complica, si no se es capaz de extraer lo esencial.

¿Crees que tú modelo es suficientemente bueno?

Hace mucho tiempo, en una de mis vidas pasadas como consultor, escuché que un responsable DS de una conocida telco, le suelta un junior algo así como que una mejora de unas décimas en la curva ROC, significaba una mejora de miles o cientos de miles de euros en su caso de uso …

Bueno, sobre la curva ROC habría mucho de que hablar, sobre todo entender bien lo que significa (que aún muchos confunde con el r-cuadrado y no tiene ná que ver), pero eso lo dejo para otra sesión. Lo cierto, es que si a mí me sueltan algo como lo anterior, es muy probable que deje de considerar a esa persona como alguien que entiende de modelos y más le valga, darle un repaso a la estadística y sobre todo al sentido común, que parece ser el menos común de los sentidos.

Para empezar a hablar, vaya por delante que en estadística pocas o más bien nunca se tienen valores absolutos, prácticamente todo son variables aleatorias que siguen una distribución más o menos compleja, en algunos casos, bajo el marco de la estadística clásica y con hipótesis más o menos fuertes, se consigue conocer para un modelo, como el lineal, la distribución de sus parámetros y por tanto se tienen intervalos de confianza y todo aquello de lo que hoy no me apetece tratar.

Tanto esos modelos, como los actuales, en todos, hay variables aleatorias y la aleatoriedad es algo, que aunque se pueda controlar más o menos, ahí está y por tanto, está en los parámetros de los modelos y por supuesto en las estimaciones o medidas de su potencia predictiva, siendo la ROC un ejemplo de éstas en el caso de modelos de variable binarias

Si os vais a mi github, cuyo enlace os dejo aquí:

https://github.com/FJROAR/Ejemplo-Blog-ROC-Distribution

He dejado unos códigos muy sencillos para analizar un dataset como es el de biopsia que está dentro de la libreria(MASS) y que está bastante trillado pero, debido a que son pocos datos y variables, creo que puede valer para la explicación de este post.

Bien en ese código hay un par de funciones que he diseñado de modo no óptimo, pero que para este caso corren adecuadamente y nos va a permitir una discusión sobre la volatilidad de la curva ROC. Dichas funciones se denominan:

genera_roc_glm(seed, df) y genera_roc_knn(seed, df)

Y lo que hacen es que toman un dataframe df ya limpio (ojo, no aseguro que funcione para cualquier df limpio, la intención aquí es explicar un concepto, no hacer algo que raye la pureza informática, … ya que no soy informático), y lo dividen en el típico train-test al 70% bajo una semilla de aleatorización que se elije en seed, dando por tanto lugar en la primera función a la curva roc que se tendría bajo una regresión logística habitual y en el caso del knn sale el valor de la roc con los parámetros por defecto que tendría el algoritmo aplicado. Además para simplificar aún más la situación se toma como variable explicativa de la target a la V1 en este primer caso para ambas funciones.

Llegados a este punto, ¿qué pasa si seed = 1? En este caso se obtiene lo siguiente:

Claro, si soy forofo del 1 en las seed y siempre lo uso, podría afirmar que a nivel de predictividad el primero modelo es mejor que el segundo, y si no miro nada más, pues ala, a tratar de defenderlo. Pero claro, ahora viene el/la forofo/a del número 10 y hace le sucede lo siguiente:

Entonces se observa que para dicho forofo/a, lo lógico sería un knn ya que su predictividad es mejor.

Bueno en este caso resulta que lo que ocurre es que la ROC es una variable aleatoria y por tanto sus valores más frecuentes estarán bajo unos intervalos cuya distribución será difícil de conocer, ya que aparte de la semilla de aleatorización, también va a depender de la separación 70-30 o 60-40 o … que se haya realizado, por tanto hacer una apuesta a un modelo en concreto porque se gane unas décima de ROC es prácticamente como tirar una moneda al aire y básicamente el histograma de cuando se generan 100 semillas y se hace la misma operación es lo que se muestra, para el caso del modelo glm y knn en el dibujo inicial. En dichos histogramas de tan sólo 100 valores (podría calcularse para más), se observa que la media y la desviación típica resultan ser las siguientes:

media glm: 0.910738 media knn: 0.906869

desviación glm: 0.016557 desviación knn: 0.018118

Nótese que gráficamente y numéricamente todo iría hacia el glm, pero claro es una muestra de sólo 100 observaciones, pero las variaciones y los saltos de valores que se da en esta sencilla distribución van desde aproximadamente 0.85 hasta algo más de 0.94 tal y como se observa a continuación:

En casos de muchas observaciones, cuando he realizado este tipo de estudios, no he visto efectos tan grandes, pero sí bastante amplios, aunque con más concentración en torno a los valores medios, con lo que hay que tener cierto cuidado cuando nos fiamos de un índice. Es cierto, que la técnica de cross-validation también puede dar una idea de cómo va a ser la variabilidad de la ROC, pero sorprende que en los proyectos de modelización, este factor no se tengan en cuenta y los que yo denomino como “preparadores de datos” que son gente que se hacen llamar DS y que lo que saben es preparar datos para meterlos en una coctelera y sacar un alto ROC o bien no se dan cuenta, o directamente no entienden los saltos que pueden dar los estadísticos que están estimando.

Y bueno, visto esto, vamos a dar una vuelta de tuerca más, supongamos que ahora en vez de 1 variable, usamos V1 y V2, a ver qué es lo que pasa si repetimos el proceso, para eso he creado las funciones:

genera_roc_glm2(seed, df) y genera_roc_knn2(seed, df)

Para no extender la exposición os hago expoiler y os dejo unas recomendaciones y consejos:

• El algoritmo puede ayudar, pero cuando se usa una variable potente, se puede pasar a otra liga, un algoritmo mejora y todos mejoran al unísono en este caso
  

• Las conclusiones se mantienen, algo más acentuadas, pero las distribuciones se superponen, hay algunos outliers, pero “no nos sacan de pobres”
  

• Este dataset está muy preparado, por eso sale tan potente, pero una vez llegado al 0.98 de ROC, poco más se va a poder mejorar
  

• Las fluctuaciones deben tenerse en cuenta, incluso en los proyecto de ML con miles de millones de datos debe controlarse los márgenes de variabilidad de la ROC, sobre todo cuando vayan a intervenir mucho dinero. Mejor dar intervalos máximo-mínimos estimados que valores cerrados que impidan la creatividad
  

• Ante modelos de predictividades parecidas, ir al más simple, si los modelos aún tienen cierta diferencia de predictividad, pero son elevadas, tomar el más simple, aunque a los “complicadores” les parecerá una “caca” porque son sencillos, os daréis cuenta que son robustos y que los podéis explicar